Consider an earnings-producing asset of unknown price S* priced using equation (1) in the tradition of Gordon (1959, 1962). Et denotes the asset’s future random earnings, and E0 (Et) their expectations.
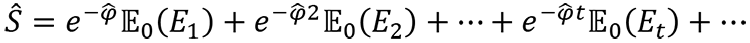
The discount rate φ̂ is constant. Let φIRR denote the unknown IRR of the asset satisfying equation (2).

Under what conditions can we be confident that φ̂≈φIRR⟹Ŝ≈S*? Is the price of the asset Ŝ necessarily close enough to is true unknown price S* if the analyst does a good job at selecting φ̂≈φIRR with φIRR unknown? The answer is no. Specifically, in the Gordon (1959, 1962) tradition, the analyst specifies E0 (Et )=E0egt with E0 known, and selects φ̂>g to ensure convergence of equation (1). If φIRR≈g with φIRR>g, then Ŝ will almost certainly be substantially different from S*, even if φ̂≈φIRR.
Numerical Illustration
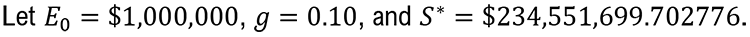
The asset’s IRR is φIRR=10.4190092146264 percent using equation (2). Because φIRR≈g, it is almost certainly the case that Ŝ≠S* even if φ̂≈φIRR. Consider two experienced analysts. They select φ̂1=10.3 percent and φ̂2=10.5 percent, respectively.
Table 1. Pricing Errors Equation (1)
The only acceptable constant discount rate, at a precision of its first decimal point (in percent, 3rd decimal of the rate), is φ̂=10.4 percent, yielding Ŝ=$244,930,575, or a 4 percent pricing error. A more precise valuation requires guessing φIRR with precision of φ̂ at its second decimal point (in percent, 4th decimal of the rate).
Explanation
Imagine a skateboarding half-pipe. Consider a small horizontal displacement of the skateboard on the flat portion of the half-pipe. The resulting vertical displacement of the skateboard is minimal. Now, consider the same small horizontal displacement on the steep portion of the half-pipe. The vertical displacement of the skateboard is large, whether uphill or downhill. Equation (1) has the shape of a skateboarding half-pipe for any given value of g, with its flat portion for g≪φIRR, and with its steep portion for g≈φIRR. For assets such that g≈φIRR, a small change in φ̂≈φIRR results in a large change in Ŝ relative to S*. None of that has anything to do with the experience of the analyst. The problem is not the analyst or his or her experience, it is the model of equation (1) and the precision it requires in its constant discount rate.
Cure and Conclusion
“Using constant discount rates can produce large misvaluations…”. Ang and Liu (2004). Table 1 illustrates that statement. A 0.2 change in the constant discount rate from 10.3 percent to 10.5 percent swings the valuation from a 35 percent overvaluation to a 16 percent undervaluation. The only way the IRR of the asset can be calculated is by solving equation (2), which requires to know the asset price S*. There is no way around that. Therefore, the only cure to the problem is to replace the model of equation (1) with the model of equation (3) or equation (4), and to specify a model for the discount rate function φ̂(t).
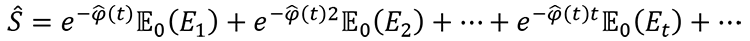
Mathematically, for any given value of g, equation (3) no longer has the shape of a half-pipe. The “flattening” of the range of the function everywhere over the domain of its discount rate argument ensures that any small change in any of the discount rates φ̂(t) results in a small change in the asset price. The cure, therefore, is to avoid a model requiring to guess the IRR of the asset to price it. The solutions offered in the modern asset pricing literature, since Merton (1973)’s ICAPM rely on equation (4), not equation (3), and are impractical for everyday use by practitioners because the function φ̂(t) is stochastic. The discount factors cannot be removed from the expectations.
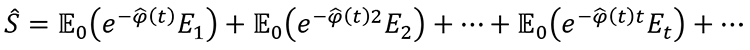
The multi-period CAPM (MCAPM”) offers a helpful implementation of equation (3). It extends the static one-period CAPM model to multi-periods, and preserves deterministic discount rates and factors, contrary to ICAPM and the plethora of modern asset pricing models developed since the 1970’s.
MCAPM can be implemented in a standard spreadsheet by anyone familiar with the use of the spreadsheet’s solver. The MCAPM discount rate curve has the general form below.

Further information concerning MCAPM is available from the author upon request.
Stay Ahead with Kroll
Valuation Services
When companies require an objective and independent assessment of value, they look to Kroll.
Transfer Pricing
Kroll's team of internationally recognized transfer pricing advisors provide the technical expertise and industry experience necessary to ensure understandable, implementable and supportable results.
